数学三角函数是什么，反三角函数基本公式大全(附2023年最新排行榜前十名单)

一、三角函数是什么？

三角函数是基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。也可以等价地用与单位圆有关的各种线段的长度来定义。

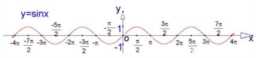
1、函数：y=sinx；

定义域：R；

值域：［-1，1］x=2kπ+π/2 时ymax=1，x=2kπ-π/2 时ymin=-1；

周期性：2π；

奇偶性：奇函数；

单调性：

在［2kπ-π/2,2kπ+π/2 ］上都是增函数；

在［2kπ+π/2 ,2kπ+2π/3］上都是减函数(k∈Z)；

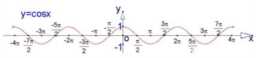
2、函数：y=cosx；

定义域：R；

值域：［-1，1］x=2kπ时ymax=1，x=2kπ+π时ymin=-1；

周期性：2π；

奇偶性：偶函数；

单调性：

在［2kπ-π,2kπ ］上都是增函数；

在［2kπ ,2kπ+π］上都是减函数(k∈Z)；

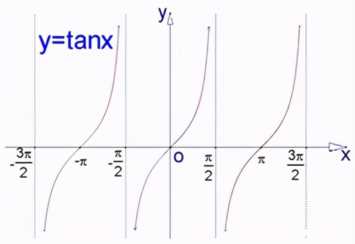
3、函数：y=tanx；

定义域：｛x｜x∈R且x≠kπ+π/2,k∈Z｝；

值域：无最大值、无最小值；

周期性：π；

奇偶性：奇函数；

单调性：在［kπ-π/2,kπ+π/2 ］上都是增函数(k∈Z)；

4、函数：y=cotx；

定义域：｛x｜x∈R且x≠kπ,k∈Z｝；

值域：无最大值、无最小值；

周期性：π；

奇偶性：奇函数；

单调性：在［kπ,kπ+π ］上都是减函数(k∈Z)；

二、三角函数的推导过程

设f(x)=sinx；(f(x+dx)-f(x))/dx=(sin(x+dx)-sinx)/dx=(sinxcosdx+sindxcosx－sinx)/dx因为dx趋近于0cosdx趋近于1(f(x+dx)-f(x))/dx=sindxcosx/dx根据重要极限sinx/x在x趋近于0时等于一，(f(x+dx)-f(x))/dx＝cosx，即sinx的导函数为cosx。

同理可得，

设f(x)=cos(f(x+dx)-f(x))/dx=(cos(x+dx)-cosx)/dx=(cosxcosdx-sinxsindx－sinx)/dx，因为dx趋近于0cosdx趋近于1(f(x+dx)-f(x))/dx=-sindxsinx/dx，根据重要极限sinx/x在x趋近于0时等于一(f(x+dx)-f(x))/dx＝-sinx即cosx的导函数为-sinx。

注：不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。然而，可导的函数一定连续；不连续的函数一定不可导。

三、三角函数必备公式

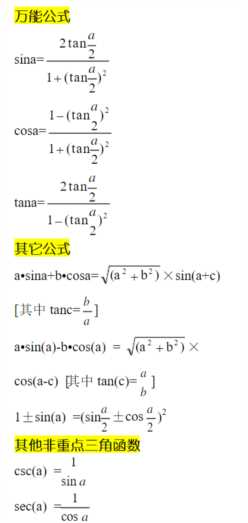
四、三角函数的难点问题?

1、三角函数图像性质的综合应用问题

三角函数图像性质的综合应用问题在高考中瓦王充当把关题的角色，难度较大，解题的关键是抓住图像上的一些特征来综合分析问题，如对称轴、对称中心、周期特征、单调区间、函数值相等或相反等。

结合对三角函数的深刻认识画出草图，寻找图中关键点时解决这类问题的较好解法。

2、射影定理化解问题

用最简单的射影定理代替计算量大的余弦定理，从而解决负责多变的三角形问题。

反三角函数的定义值及值域

这里简单总结了反三角函数的定义、其对应的三角函数、其定义域、值域，其后利用反函数求导法则完成了所有反函数求导公式的推导证明。不难看出上述推导过程其实都并不复杂（除反正割、反余割函数外），若能熟练使用各种三角函数变换技巧则能轻松完成所有证明。

反三角函数的导数及其定义域

arcsin（x）导数

arccos（x）导数

arctan（x）导数

arcsec（x）导数